Ansa Custom Parameters and Formulas
1. Define parameters
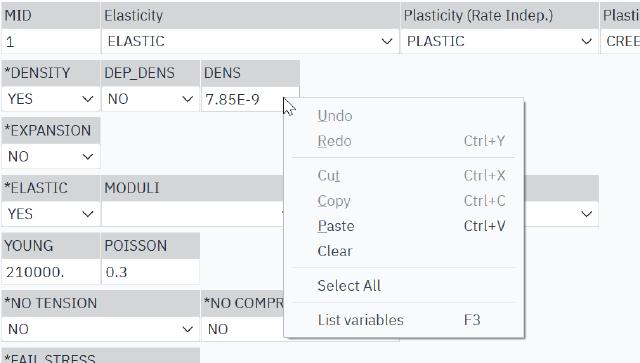
Custom parameters in ANSA are relatively simple. Right-click in the input box to open the menu and select List variables, then create a new variable in the A_PARAMETERs dialog and assign a name to that variable.
For example, here the material parameter is assigned as a custom parameter:
-
Right-click to select the
list variables.