Speaking of matrices, anyone who studies science and engineering will think of the fear of being dominated by linear algebra classes. Matrix multiplication operations are indispensable for various industrial and scientific research numerical calculations, and are also used in various benchmarking software. The time consumption of matrix multiplication operations is also an important indicator for judging the floating-point operation performance of computers. The purpose of this article is to verify the performance differences of various implementation methods through matrix multiplication operations, and compare the performance differences of different computing platforms to provide a reference for high-performance computing development.
1. Matrix multiplication algorithm
Matrix multiplication is also called matrix dot multiplication, which can be represented by the following figure 1. It is usually formed by multiplying and accumulating the elements of the corresponding rows of matrix A and the corresponding columns of matrix B to form the values of the corresponding rows and columns of matrix C. The number of columns of matrix A must be equal to the number of rows of matrix B, and the size of matrix C is equal to the number of rows of matrix B × the number of columns of matrix A.
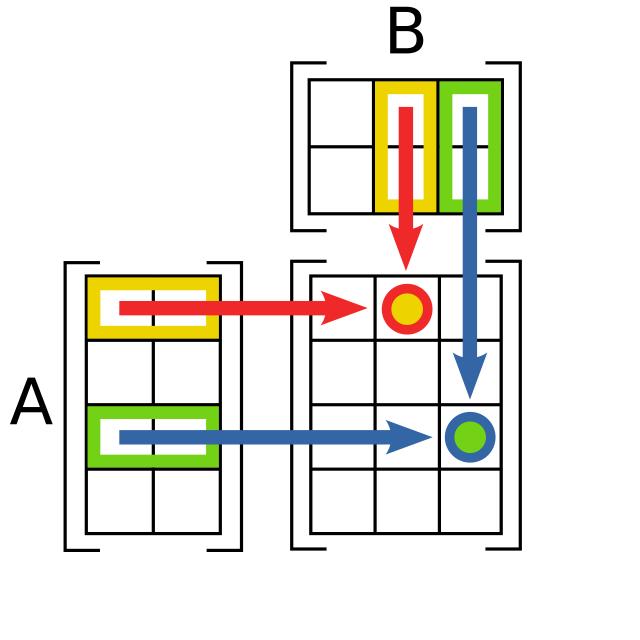
Using C language to represent an M×N matrix dot multiplication with an N×T matrix, it is generally written in the form of 3 layers of nested loops.
...
for (int i = 0; i < M; i++)
{
for (int j = 0; j < T; j++)
{
C[i,j] = 0.0;
for (int k = 0; k < N; k++)
{
C[i,j] += A[i,k] * B[k,j];
}
}
}
...
It is generally believed that the number of multiplications of an N×N dimensional matrix is N to the power of 3, and the computational complexity is expressed as O(n3). There are also some algorithms that convert some of the multiplication operations into additions, reducing the number of multiplication operations. For example, the Strassen algorithm2 has a theoretical computational complexity of only O(n2.807), which reduces the time spent on multiplying large matrices. Newer algorithms such as the Coppersmith-Winograd method are said to have a computational complexity of only O(n2.3727). This difference in algorithms is not discussed in this article.
2. Parallelization of nested loops
Modern computer processors are generally multi-core. To fully utilize the processor performance, it is a good option to use parallel libraries such as OpenMP to parallelize the calculation program. It is meaningless to use a single core to solve the nested loop. I will not demonstrate it here. If you are interested, you can remove the parallel library from the following code and compile and calculate it.
2.1 C Implementation
The C implementation is very simple, using three layers of nested loops to implement the matrix multiplication algorithm. Here, openmp is used to merge the first two layers of loops and assign them to different threads for calculation 3, so as to fully utilize the performance of multi-core processors. The following is the sample code of openmp.c.
#include <omp.h>
void matrix_multiply_float(int n, float A[], float B[], float C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
C[i * n + j] = 0;
for (int k = 0; k < n; k++)
{
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
void matrix_multiply_double(int n, double A[], double B[], double C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
C[i * n + j] = 0;
for (int k = 0; k < n; k++)
{
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
In main.c, some command line switches are defined, and users can customize matrix size, number of loops, calculation accuracy, etc. A performance parameter, GFLOPs, is defined here to measure the ability to perform floating-point operations per unit time. 1 GFLOPs is equivalent to performing 109 floating-point operations in 1 second.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <math.h>
#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define MIN(a, b) ((a) < (b) ? (a) : (b))
extern void matrix_multiply_float(int n, float A[], float B[], float C[]);
extern void matrix_multiply_double(int n, double A[], double B[], double C[]);
// Initialize matrix
void initialize_matrix_float(int n, float matrix[])
{
srand((unsigned)time(NULL));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
matrix[i * n + j] = rand() / (float)(RAND_MAX);
}
}
}
void initialize_matrix_double(int n, double matrix[])
{
srand((unsigned)time(NULL));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
matrix[i * n + j] = rand() / (double)(RAND_MAX);
}
}
}
// Execute matrix multiply and print results
int execute_float(int dim, int loop_num, double *ave_gflops, double *max_gflops, double *ave_time, double *min_time)
{
// Use volatile to prevent compiler optimizations
volatile float *a, *b, *c;
struct timespec start_ns, end_ns;
double cpu_time;
for (int i = 0; i < loop_num; i++)
{
a = (float *)malloc(dim * dim * sizeof(float));
b = (float *)malloc(dim * dim * sizeof(float));
c = (float *)malloc(dim * dim * sizeof(float));
if (a == NULL || b == NULL || c == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return 0;
}
initialize_matrix_float(dim, a);
initialize_matrix_float(dim, b);
timespec_get(&start_ns, TIME_UTC);
matrix_multiply_float(dim, a, b, c);
timespec_get(&end_ns, TIME_UTC);
cpu_time = (end_ns.tv_sec - start_ns.tv_sec) + (end_ns.tv_nsec - start_ns.tv_nsec) / 1e9;
double gflops = 1e-9 * dim * dim * dim * 2 / cpu_time;
printf("%d\t: %d x %d Matrix multiply wall time : %.6fs(%.3fGflops)\n", i + 1, dim, dim, cpu_time, gflops);
free(a);
free(b);
free(c);
*ave_gflops += gflops;
*max_gflops = MAX(*max_gflops, gflops);
*ave_time += cpu_time;
*min_time = MIN(*min_time, cpu_time);
}
*ave_gflops /= loop_num;
*ave_time /= loop_num;
return 1;
}
int execute_double(int dim, int loop_num, double *ave_gflops, double *max_gflops, double *ave_time, double *min_time)
{
// Use volatile to prevent compiler optimizations
volatile double *a, *b, *c;
struct timespec start_ns, end_ns;
double cpu_time;
for (int i = 0; i < loop_num; i++)
{
a = (double *)malloc(dim * dim * sizeof(double));
b = (double *)malloc(dim * dim * sizeof(double));
c = (double *)malloc(dim * dim * sizeof(double));
if (a == NULL || b == NULL || c == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return 0;
}
initialize_matrix_double(dim, a);
initialize_matrix_double(dim, b);
timespec_get(&start_ns, TIME_UTC);
matrix_multiply_double(dim, a, b, c);
timespec_get(&end_ns, TIME_UTC);
cpu_time = (end_ns.tv_sec - start_ns.tv_sec) + (end_ns.tv_nsec - start_ns.tv_nsec) / 1e9;
double gflops = 1e-9 * dim * dim * dim * 2 / cpu_time;
printf("%d\t: %d x %d Matrix multiply wall time : %.6fs(%.3fGflops)\n", i + 1, dim, dim, cpu_time, gflops);
free(a);
free(b);
free(c);
*ave_gflops += gflops;
*max_gflops = MAX(*max_gflops, gflops);
*ave_time += cpu_time;
*min_time = MIN(*min_time, cpu_time);
}
*ave_gflops /= loop_num;
*ave_time /= loop_num;
return 1;
}
int main(int argc, char *argv[])
{
int n = 10; // Default matrix size exponent
int loop_num = 5; // Number of iterations for averaging
double ave_gflops = 0.0, max_gflops = 0.0; // Average and maximum Gflops
double ave_time = 0.0, min_time = 1e9; // Average and minimum time
int use_double = 0; // Default to float precision
// Help message
if (argc == 1 || (argc == 2 && (strcmp(argv[1], "-h") == 0 || strcmp(argv[1], "--help") == 0)))
{
printf("Usage: %s [-n SIZE] [-l LOOP_NUM] [-float|-double]\n", argv[0]);
printf(" -n SIZE Specify matrix size, like 2^SIZE (default: 10)\n");
printf(" -l LOOP_NUM Specify number of iterations (default: 5)\n");
printf(" -float Use float precision (default)\n");
printf(" -double Use double precision\n");
printf(" -h, --help Show this help message\n");
return 0;
}
// Parse -n, -l, -float, -double options
int double_flag = 0, float_flag = 0;
for (int argi = 1; argi < argc; ++argi)
{
if (strcmp(argv[argi], "-n") == 0 && argi + 1 < argc)
{
n = atoi(argv[argi + 1]);
argi++;
}
else if (strcmp(argv[argi], "-l") == 0 && argi + 1 < argc)
{
loop_num = atoi(argv[argi + 1]);
argi++;
}
else if (strcmp(argv[argi], "-double") == 0)
{
double_flag = 1;
}
else if (strcmp(argv[argi], "-float") == 0)
{
float_flag = 1;
}
}
if (double_flag && float_flag)
{
fprintf(stderr, "Error: Cannot specify both -double and -float options.\n");
return 1;
}
use_double = double_flag ? 1 : 0;
int dim = (int)pow(2, n);
if (use_double)
{
printf("Using double precision for matrix multiplication.\n");
execute_double(dim, loop_num, &ave_gflops, &max_gflops, &ave_time, &min_time);
}
else
{
printf("Using float precision for matrix multiplication.\n");
execute_float(dim, loop_num, &ave_gflops, &max_gflops, &ave_time, &min_time);
}
printf("Average Gflops: %.3f, Max Gflops: %.3f\n", ave_gflops, max_gflops);
printf("Average Time: %.6fs, Min Time: %.6fs\n", ave_time, min_time);
return 0;
}
CMake is used here, and CMakeLists.txt tells the compiler how to include the openmp header file and link to it.
cmake_minimum_required(VERSION 3.13)
project(openmp LANGUAGES C)
set(CMAKE_C_STANDARD 11)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_C_COMPILER_FRONTEND_VARIANT}_${CMAKE_C_COMPILER_ID}_${CMAKE_C_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
find_package(OpenMP REQUIRED)
set(SRC_LIST
src/main.c
src/openmp.c
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
OpenMP::OpenMP_C
)
The Release program compiled by clang-cl of vs2022 on Windows platform has the following execution effect:
PS D:\example\efficiency_v3\c\openmp\build\Release> ."D:/example/efficiency_v3/c/openmp/build/Release/openmp_msvc_clang_19.1.5.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.362688s(5.921Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.304758s(7.047Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.314348s(6.832Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.294248s(7.298Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.294496s(7.292Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.306986s(6.995Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.320405s(6.702Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.278521s(7.710Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.294080s(7.302Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.338626s(6.342Gflops)
Average Gflops: 6.944, Max Gflops: 7.710
Average Time: 0.310916s, Min Time: 0.278521s
PS D:\example\efficiency_v3\c\openmp\build\Release> ."D:/example/efficiency_v3/c/openmp/build/Release/openmp_msvc_clang_19.1.5.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.353909s(6.068Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.319001s(6.732Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.329514s(6.517Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.381114s(5.635Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.349447s(6.145Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.370087s(5.803Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.349626s(6.142Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.370023s(5.804Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.364005s(5.900Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.344441s(6.235Gflops)
Average Gflops: 6.098, Max Gflops: 6.732
Average Time: 0.353117s, Min Time: 0.319001s
Compiled using MSYS2’s clang64 toolchain, the Release program execution results are as follows:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_clang_20.1.7.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.344437s(6.235Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.327010s(6.567Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.367141s(5.849Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.358603s(5.988Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.362182s(5.929Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.338947s(6.336Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.334758s(6.415Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.331219s(6.484Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.343316s(6.255Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.324451s(6.619Gflops)
Average Gflops: 6.268, Max Gflops: 6.619
Average Time: 0.343206s, Min Time: 0.324451s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_clang_20.1.7.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.447118s(4.803Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.423630s(5.069Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.365229s(5.880Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.355163s(6.046Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.443296s(4.844Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.310319s(6.920Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.366405s(5.861Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.369704s(5.809Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.382898s(5.608Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.367266s(5.847Gflops)
Average Gflops: 5.669, Max Gflops: 6.920
Average Time: 0.383103s, Min Time: 0.310319s
Switch to MSYS2’s ucrt64 toolchain to compile, and the Release program execution effect is as follows:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.308967s(6.951Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.267709s(8.022Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.278587s(7.708Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.263047s(8.164Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.262595s(8.178Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.264196s(8.128Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.273148s(7.862Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.262910s(8.168Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.277290s(7.745Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.274961s(7.810Gflops)
Average Gflops: 7.874, Max Gflops: 8.178
Average Time: 0.273341s, Min Time: 0.262595s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.314685s(6.824Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.290665s(7.388Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.304162s(7.060Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.315041s(6.817Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.306290s(7.011Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.356495s(6.024Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.310081s(6.926Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.301022s(7.134Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.317229s(6.769Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.307106s(6.993Gflops)
Average Gflops: 6.895, Max Gflops: 7.388
Average Time: 0.312278s, Min Time: 0.290665s
The performance of the gcc compiler on the Windows platform is slightly better. The computing performance of the three is basically at the same level, and the difference is small and can be ignored.
The above are all calculated results on the AMD AI 9 365w processor, and all cores and hyperthreads are basically fully utilized during the calculation process. The calculation results shown in this article, unless otherwise specified, are the results output by running on this processor.
2.2 Fortran Implementation
Fortran has a built-in matrix operation function matmul. We will not consider the algorithm optimization of built-in functions here. The three-layer loop nesting implemented in C is implemented in Fortran, and then accelerated by openmp.
The function implemented by main.f90 is the same as that of main.c implemented in C.
program main
implicit none
external matrix_multiply_float, matrix_multiply_double
integer :: n = 10
integer :: loop_num = 5
real :: ave_gflops = 0.0, max_gflops = 0.0
real :: ave_time = 0.0, min_time = 1e9
logical :: use_double = .false.
integer :: argi, i, dim
character(len=100) :: arg
logical :: double_set = .false., float_set = .false.
if (command_argument_count() == 0) then
call print_help()
stop
end if
argi = 1
do while (argi <= command_argument_count())
call get_command_argument(argi, arg)
if (trim(arg) == '-n' .and. argi + 1 <= command_argument_count()) then
argi = argi + 1
call get_command_argument(argi, arg)
read(arg, *) n
else if (trim(arg) == '-l' .and. argi + 1 <= command_argument_count()) then
argi = argi + 1
call get_command_argument(argi, arg)
read(arg, *) loop_num
else if (trim(arg) == '-double') then
double_set = .true.
use_double = .true.
else if (trim(arg) == '-float') then
float_set = .true.
use_double = .false.
else if (trim(arg) == '-h' .or. trim(arg) == '--help') then
call print_help()
stop
end if
if (double_set .and. float_set) then
print *, "Error: Cannot specify both -double and -float options."
stop
end if
argi = argi + 1
end do
dim = 2**n
if (use_double) then
call perform_double(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
else
call perform_float(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
end if
ave_gflops = ave_gflops / loop_num
ave_time = ave_time / loop_num
print '(A, F8.3, A, F8.3)', 'Average Gflops: ', ave_gflops, ', Max Gflops: ', max_gflops
print '(A, F10.6, A, F10.6, A)', 'Average Time: ', ave_time, 's, Min Time: ', min_time, 's'
contains
subroutine print_help()
print *, 'Usage: program_name [-n SIZE] [-l LOOP_NUM] [-float|-double]'
print *, ' -n SIZE Specify matrix size, like 2^SIZE (default: 10)'
print *, ' -l LOOP_NUM Specify number of iterations (default: 5)'
print *, ' -float Use real*32 precision (default)'
print *, ' -double Use real*64 precision'
print *, ' -h, --help Show this help message'
end subroutine print_help
subroutine initialize_matrix_float(n, matrix)
integer, intent(in) :: n
real, intent(out) :: matrix(n, n)
integer :: i, j
real :: rand
call random_seed()
do i = 1, n
do j = 1, n
call random_number(rand)
matrix(i, j) = rand
end do
end do
end subroutine initialize_matrix_float
subroutine initialize_matrix_double(n, matrix)
integer, intent(in) :: n
real*8, intent(out) :: matrix(n, n)
integer :: i, j
real*8 :: rand
call random_seed()
do i = 1, n
do j = 1, n
call random_number(rand)
matrix(i, j) = rand
end do
end do
end subroutine initialize_matrix_double
subroutine perform_double(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
integer, intent(in) :: dim, loop_num
real, intent(inout) :: ave_gflops, max_gflops, ave_time
real, intent(inout) :: min_time
real*8, allocatable :: a_double(:, :), b_double(:, :), c_double(:, :)
real :: gflops
integer*8 :: i, start_count(1), end_count(1), count_rate(1)
real :: elapsed_time
print *, 'Using real*64 precision for matrix multiplication.'
allocate(a_double(dim, dim), b_double(dim, dim), c_double(dim, dim))
do i = 1, loop_num
call initialize_matrix_double(dim, a_double)
call initialize_matrix_double(dim, b_double)
call system_clock(count=start_count(1), count_rate=count_rate(1))
call matrix_multiply_double(dim, a_double, b_double, c_double)
call system_clock(count=end_count(1))
elapsed_time = real(end_count(1) - start_count(1)) / real(count_rate(1))
gflops = 1e-9 * dim * dim * dim * 2 / elapsed_time
print '(I8, A, I0, A, I0, A, F10.6, A, F8.3, A)', i, ' : ', dim, ' x ', dim, ' Matrix multiply wall time : ', elapsed_time, 's(', gflops, 'Gflops)'
ave_gflops = ave_gflops + gflops
max_gflops = max(max_gflops, gflops)
ave_time = ave_time + elapsed_time
min_time = min(min_time, elapsed_time)
end do
deallocate(a_double, b_double, c_double)
end subroutine perform_double
subroutine perform_float(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
integer, intent(in) :: dim, loop_num
real, intent(inout) :: ave_gflops, max_gflops, ave_time
real, intent(inout) :: min_time
real*4, allocatable :: a_float(:, :), b_float(:, :), c_float(:, :)
real :: gflops
integer*8 :: i, start_count(1), end_count(1), count_rate(1)
real :: elapsed_time
print *, 'Using real*32 precision for matrix multiplication.'
allocate(a_float(dim, dim), b_float(dim, dim), c_float(dim, dim))
do i = 1, loop_num
call initialize_matrix_float(dim, a_float)
call initialize_matrix_float(dim, b_float)
call system_clock(count=start_count(1), count_rate=count_rate(1))
call matrix_multiply_float(dim, a_float, b_float, c_float)
call system_clock(count=end_count(1))
elapsed_time = real(end_count(1) - start_count(1)) / real(count_rate(1))
gflops = 1e-9 * dim * dim * dim * 2 / elapsed_time
print '(I8, A, I0, A, I0, A, F10.6, A, F8.3, A)', i, ' : ', dim, ' x ', dim, ' Matrix multiply wall time : ', elapsed_time, 's(', gflops, 'Gflops)'
ave_gflops = ave_gflops + gflops
max_gflops = max(max_gflops, gflops)
ave_time = ave_time + elapsed_time
min_time = min(min_time, elapsed_time)
end do
deallocate(a_float, b_float, c_float)
end subroutine perform_float
end program main
omp.f90 is a concrete implementation of the three-layer loop algorithm, and also uses OpenMP to expand the first two layers of loops to achieve parallelization.
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer, intent(in) :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
integer :: i, j, k
c = 0.0
!$omp parallel do private(i, j, k) shared(a, b, c, n) collapse(2)
do i = 1, n
do j = 1, n
do k = 1, n
c(i, j) = c(i, j) + a(i, k) * b(k, j)
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer, intent(in) :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
integer :: i, j, k
c = 0.0d0
!$omp parallel do private(i, j, k) shared(a, b, c, n) collapse(2)
do i = 1, n
do j = 1, n
do k = 1, n
c(i, j) = c(i, j) + a(i, k) * b(k, j)
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_double
The contents of the CMakeLists.txt file are shown below:
cmake_minimum_required(VERSION 3.13)
project(openmp-fortran LANGUAGES Fortran)
set(CMAKE_Fortran_STANDARD 2008)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_Fortran_COMPILER_FRONTEND_VARIANT}_${CMAKE_Fortran_COMPILER_ID}_${CMAKE_Fortran_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
# Enable OpenMP
find_package(OpenMP REQUIRED)
set(SRC_LIST
src/main.f90
src/omp.f90
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
OpenMP::OpenMP_Fortran
)
Compile using Intel oneAPI ifx, and the Release program execution effect is as follows:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build\Release> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/Release/openmp-fortran_msvc_intelllvm_2025.1.1.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.299000s( 7.182Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.284000s( 7.562Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.337000s( 6.372Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.310000s( 6.927Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.321000s( 6.690Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.358000s( 5.999Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.290000s( 7.405Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.312000s( 6.883Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.301000s( 7.134Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.290000s( 7.405Gflops)
Average Gflops: 6.956, Max Gflops: 7.562
Average Time: 0.310200s, Min Time: 0.284000s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build\Release> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/Release/openmp-fortran_msvc_intelllvm_2025.1.1.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.391000s( 5.492Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.362000s( 5.932Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.334000s( 6.430Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.393000s( 5.464Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.331000s( 6.488Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.357000s( 6.015Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.366000s( 5.867Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.345000s( 6.225Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.341000s( 6.298Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.359000s( 5.982Gflops)
Average Gflops: 6.019, Max Gflops: 6.488
Average Time: 0.357900s, Min Time: 0.331000s
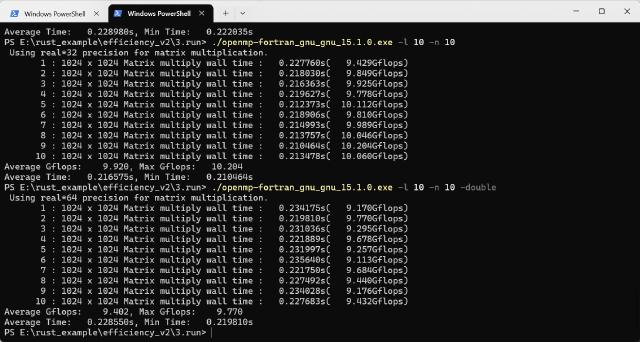
Compiled using MSYS2’s ucrt64 toolchain, the Release program execution results are as follows:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.224624s( 9.560Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.224959s( 9.546Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.228968s( 9.379Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.238853s( 8.991Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.216879s( 9.902Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.212407s( 10.110Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.233809s( 9.185Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.240426s( 8.932Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.241291s( 8.900Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.222414s( 9.655Gflops)
Average Gflops: 9.416, Max Gflops: 10.110
Average Time: 0.228463s, Min Time: 0.212407s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.258885s( 8.295Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.299699s( 7.165Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.298025s( 7.206Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.291631s( 7.364Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.271050s( 7.923Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.330989s( 6.488Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.278846s( 7.701Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.281121s( 7.639Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.288999s( 7.431Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.318669s( 6.739Gflops)
Average Gflops: 7.395, Max Gflops: 8.295
Average Time: 0.291792s, Min Time: 0.258885s
The result of running on AMD processor shows that Intel ifx version is slower than gcc version, and this is also true for multiple attempts.
The generated program is copied to Intel workstation (Xeon Gold 6226R) and the running time of both versions is basically the same. It is doubtful whether Intel compiler has made some negative optimization for AMD platform.

2.3 Rust implementation
There is no native implementation of openmp in rust, but there is a parallel library rayon with similar functions. Here, rust+rayon is used to implement a three-layer loop nesting algorithm.
main.rs implements the same function as main.c.
mod matmul;
use matmul::{matrix_multiply_double, matrix_multiply_float};
use clap::{Arg, ArgAction, Command};
use rand::prelude::*;
use std::time::Instant;
fn initialize_matrix_float(n: usize, matrix: &mut [f32]) {
let mut rng = rand::rng();
for i in 0..n * n {
matrix[i] = rng.random::<f32>();
}
}
fn initialize_matrix_double(n: usize, matrix: &mut [f64]) {
let mut rng = rand::rng();
for i in 0..n * n {
matrix[i] = rng.random::<f64>();
}
}
fn execute_float(dim: usize, loop_num: usize) -> (f64, f64, f64, f64) {
let mut ave_gflops: f64 = 0.0;
let mut max_gflops: f64 = 0.0;
let mut ave_time: f64 = 0.0;
let mut min_time = f64::MAX;
for i in 0..loop_num {
let mut a = vec![0.0; dim * dim];
let mut b = vec![0.0; dim * dim];
let mut c = vec![0.0; dim * dim];
initialize_matrix_float(dim, &mut a);
initialize_matrix_float(dim, &mut b);
let start = Instant::now();
matrix_multiply_float(dim, &a, &b, &mut c);
let cpu_time = start.elapsed().as_secs_f64();
let gflops = 2.0 * (dim * dim * dim) as f64 / cpu_time / 1e9;
println!(
"{}\t: {} x {} Matrix multiply wall time : {:.6}s({:.3}Gflops)",
i + 1,
dim,
dim,
cpu_time,
gflops
);
ave_gflops += gflops;
max_gflops = max_gflops.max(gflops);
ave_time += cpu_time;
min_time = min_time.min(cpu_time);
}
ave_gflops /= loop_num as f64;
ave_time /= loop_num as f64;
(ave_gflops, max_gflops, ave_time, min_time)
}
fn execute_double(dim: usize, loop_num: usize) -> (f64, f64, f64, f64) {
let mut ave_gflops: f64 = 0.0;
let mut max_gflops: f64 = 0.0;
let mut ave_time: f64 = 0.0;
let mut min_time = f64::MAX;
for i in 0..loop_num {
let mut a = vec![0.0; dim * dim];
let mut b = vec![0.0; dim * dim];
let mut c = vec![0.0; dim * dim];
initialize_matrix_double(dim, &mut a);
initialize_matrix_double(dim, &mut b);
let start = Instant::now();
matrix_multiply_double(dim, &a, &b, &mut c);
let cpu_time = start.elapsed().as_secs_f64();
let gflops = 2.0 * (dim * dim * dim) as f64 / cpu_time / 1e9;
println!(
"{}\t: {} x {} Matrix multiply wall time : {:.6}s({:.3}Gflops)",
i + 1,
dim,
dim,
cpu_time,
gflops
);
ave_gflops += gflops;
max_gflops = max_gflops.max(gflops);
ave_time += cpu_time;
min_time = min_time.min(cpu_time);
}
ave_gflops /= loop_num as f64;
ave_time /= loop_num as f64;
(ave_gflops, max_gflops, ave_time, min_time)
}
fn main() {
let matches = Command::new("rayon-rs")
.version("0.1.0")
.author("AndrewMoa")
.about("Matrix multiplication benchmark")
.arg(
Arg::new("size")
.short('n')
.long("size")
.help("Matrix size exponent (size = 2^n)")
.default_value("10"),
)
.arg(
Arg::new("loops")
.short('l')
.long("loops")
.help("Number of iterations")
.default_value("5"),
)
.arg(
Arg::new("f64")
.short('d')
.long("f64")
.help("Use float64 precision")
.action(ArgAction::SetTrue),
)
.arg(
Arg::new("f32")
.short('f')
.long("f32")
.help("Use float32 precision (default)")
.action(ArgAction::SetTrue),
)
.get_matches();
let n: usize = matches
.get_one::<String>("size")
.unwrap()
.parse()
.expect("Invalid size exponent");
let loop_num: usize = matches
.get_one::<String>("loops")
.unwrap()
.parse()
.expect("Invalid loop count");
let use_double = matches.get_flag("f64");
let use_float = matches.get_flag("f32");
if use_double && use_float {
eprintln!("Error: Cannot specify both --f64 and --f32");
std::process::exit(1);
}
let dim = 2usize.pow(n as u32);
if use_double {
println!("Using f64 precision for matrix multiplication.");
let (ave_gflops, max_gflops, ave_time, min_time) = execute_double(dim, loop_num);
println!(
"Average Gflops: {:.3}, Max Gflops: {:.3}",
ave_gflops, max_gflops
);
println!("Average Time: {:.6}s, Min Time: {:.6}s", ave_time, min_time);
} else {
println!("Using f32 precision for matrix multiplication.");
let (ave_gflops, max_gflops, ave_time, min_time) = execute_float(dim, loop_num);
println!(
"Average Gflops: {:.3}, Max Gflops: {:.3}",
ave_gflops, max_gflops
);
println!("Average Time: {:.6}s, Min Time: {:.6}s", ave_time, min_time);
}
}
The specific algorithm is implemented in the matmul.rs file. Here, a two-layer loop is used instead of a three-layer loop, and then the outermost loop is expanded through rayon to achieve parallelization. The actual effect is similar to openmp.
use rayon::prelude::*;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
c.par_iter_mut().enumerate().for_each(|(idx, c_ij)| {
let i = idx / n;
let j = idx % n;
*c_ij = 0.0;
for k in 0..n {
*c_ij += a[i * n + k] * b[k * n + j];
}
});
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
c.par_iter_mut().enumerate().for_each(|(idx, c_ij)| {
let i = idx / n;
let j = idx % n;
*c_ij = 0.0;
for k in 0..n {
*c_ij += a[i * n + k] * b[k * n + j];
}
});
}
The configuration file Cargo.toml file is as follows:
[package]
name = "rayon-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
rand = "0.9.1"
rayon = "1.10.0"
Compiled using the msvc toolchain on the Windows platform, the Release program has the following effects:
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\rayon-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.183645s(11.694Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.189942s(11.306Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.186613s(11.508Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.190823s(11.254Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.197830s(10.855Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.194282s(11.053Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.199380s(10.771Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.198576s(10.814Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.190201s(11.291Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.195518s(10.984Gflops)
Average Gflops: 11.153, Max Gflops: 11.694
Average Time: 0.192681s, Min Time: 0.183645s
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\rayon-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.188721s(11.379Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.186753s(11.499Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.206919s(10.378Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.197388s(10.879Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.196899s(10.907Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.206537s(10.398Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.200781s(10.696Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.191448s(11.217Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.192770s(11.140Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.178019s(12.063Gflops)
Average Gflops: 11.056, Max Gflops: 12.063
Average Time: 0.194624s, Min Time: 0.178019s
3. 3. Matrix Block Parallelization
When directly solving a large matrix, in order to improve the solving efficiency, the large matrix can be divided into small blocks for solving. This can improve the cache hit rate and improve the computing performance to a certain extent.
3.1 Matrix block C implementation
Based on the implementation in 2.1, change the contents of the openmp.c file as follows, and keep the contents of other files unchanged.
#include <omp.h>
#include <math.h>
//Block size, adjusted according to cache size
#define BLOCK_SIZE 8
void matrix_multiply_float(int n, float A[], float B[], float C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i_block = 0; i_block < n; i_block += BLOCK_SIZE) {
for (int j_block = 0; j_block < n; j_block += BLOCK_SIZE) {
for (int k_block = 0; k_block < n; k_block += BLOCK_SIZE) {
int i_end = fmin(i_block + BLOCK_SIZE, n);
int j_end = fmin(j_block + BLOCK_SIZE, n);
int k_end = fmin(k_block + BLOCK_SIZE, n);
for (int i = i_block; i < i_end; i++) {
for (int j = j_block; j < j_end; j++) {
for (int k = k_block; k < k_end; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
}
}
}
void matrix_multiply_double(int n, double A[], double B[], double C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i_block = 0; i_block < n; i_block += BLOCK_SIZE) {
for (int j_block = 0; j_block < n; j_block += BLOCK_SIZE) {
for (int k_block = 0; k_block < n; k_block += BLOCK_SIZE) {
int i_end = fmin(i_block + BLOCK_SIZE, n);
int j_end = fmin(j_block + BLOCK_SIZE, n);
int k_end = fmin(k_block + BLOCK_SIZE, n);
for (int i = i_block; i < i_end; i++) {
for (int j = j_block; j < j_end; j++) {
for (int k = k_block; k < k_end; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
}
}
}
Compiled using MSYS2’s ucrt64 toolchain on Windows, the Release program execution results are as follows:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.058133s(36.941Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.060944s(35.237Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.060845s(35.294Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.060216s(35.663Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.061135s(35.127Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.060427s(35.539Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.059523s(36.078Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.060110s(35.726Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.062199s(34.526Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.059708s(35.966Gflops)
Average Gflops: 35.610, Max Gflops: 36.941
Average Time: 0.060324s, Min Time: 0.058133s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.065988s(32.544Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.056852s(37.773Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.059504s(36.090Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.053153s(40.402Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.057459s(37.374Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.053974s(39.787Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.055030s(39.024Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.053222s(40.349Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.054025s(39.750Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.053405s(40.211Gflops)
Average Gflops: 38.330, Max Gflops: 40.402
Average Time: 0.056261s, Min Time: 0.053153s
Compared with the loop nesting algorithm, the performance is greatly improved after the block division. The block size is related to the hardware platform, which directly affects the cache hit rate and thus affects the computing performance. A lot of tests are needed to determine the most appropriate block size.
3.2 Matrix block fortran implementation
Based on the content of 2.2, only the omp.f90 file is changed and the matrix blocking algorithm is added.
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer, intent(in) :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
integer :: i, j, k, bi, bj, bk, block_size
real*4 :: temp
! Define block size, adjust according to cache situation
block_size = 8
c = 0.0
!$omp parallel do private(bi, bj, bk, i, j, k, temp) shared(a, b, c, n, block_size)
do bi = 1, n, block_size
do bj = 1, n, block_size
do bk = 1, n, block_size
do i = bi, min(bi + block_size - 1, n)
do j = bj, min(bj + block_size - 1, n)
temp = c(i, j)
do k = bk, min(bk + block_size - 1, n)
temp = temp + a(i, k) * b(k, j)
end do
c(i, j) = temp
end do
end do
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer, intent(in) :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
integer :: i, j, k, bi, bj, bk, block_size
real*8 :: temp
block_size = 8
c = 0.0d0
!$omp parallel do private(bi, bj, bk, i, j, k, temp) shared(a, b, c, n, block_size)
do bi = 1, n, block_size
do bj = 1, n, block_size
do bk = 1, n, block_size
do i = bi, min(bi + block_size - 1, n)
do j = bj, min(bj + block_size - 1, n)
temp = c(i, j)
do k = bk, min(bk + block_size - 1, n)
temp = temp + a(i, k) * b(k, j)
end do
c(i, j) = temp
end do
end do
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_double
Compiled using MSYS2’s ucrt64 toolchain on Windows, the Release program execution results are as follows:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.091248s( 23.535Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.082953s( 25.888Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.080934s( 26.534Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.078231s( 27.451Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.076461s( 28.086Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.078698s( 27.288Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.077900s( 27.567Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.079131s( 27.138Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.083838s( 25.615Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.078336s( 27.414Gflops)
Average Gflops: 26.651, Max Gflops: 28.086
Average Time: 0.080773s, Min Time: 0.076461s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.087275s( 24.606Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.080483s( 26.682Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.079304s( 27.079Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.080373s( 26.719Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.076651s( 28.016Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.080497s( 26.678Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.097153s( 22.104Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.085253s( 25.190Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.085751s( 25.043Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.098205s( 21.867Gflops)
Average Gflops: 25.399, Max Gflops: 28.016
Average Time: 0.085094s, Min Time: 0.076651s
The performance improvement depends on the block size. You can adjust the block size to slowly find the most suitable parameters.
3.3 Matrix block rust implementation
Similarly, based on 2.3, only the matmul.rs file is changed here.
use rayon::prelude::*;
// Defining the block size
const BLOCK_SIZE: usize = 8;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
c.par_chunks_mut(n).enumerate().for_each(|(i, c_row)| {
for bj in (0..n).step_by(BLOCK_SIZE) {
for bk in (0..n).step_by(BLOCK_SIZE) {
for j in bj..(bj + BLOCK_SIZE).min(n) {
for k in bk..(bk + BLOCK_SIZE).min(n) {
c_row[j] += a[i * n + k] * b[k * n + j];
}
}
}
}
});
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
c.par_chunks_mut(n).enumerate().for_each(|(i, c_row)| {
for bj in (0..n).step_by(BLOCK_SIZE) {
for bk in (0..n).step_by(BLOCK_SIZE) {
for j in bj..(bj + BLOCK_SIZE).min(n) {
for k in bk..(bk + BLOCK_SIZE).min(n) {
c_row[j] += a[i * n + k] * b[k * n + j];
}
}
}
}
});
}
Compiled using the msvc toolchain under Windows, the Release program has the following effects:
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.03s
Running `target\release\rayon-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.113868s(18.859Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.116698s(18.402Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.125060s(17.172Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.125669s(17.088Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.116527s(18.429Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.114784s(18.709Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.117369s(18.297Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.114227s(18.800Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.118140s(18.177Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.115756s(18.552Gflops)
Average Gflops: 18.249, Max Gflops: 18.859
Average Time: 0.117810s, Min Time: 0.113868s
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.03s
Running `target\release\rayon-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.120614s(17.805Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.128292s(16.739Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.122600s(17.516Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.118252s(18.160Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.127342s(16.864Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.121794s(17.632Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.130288s(16.483Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.137106s(15.663Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.130548s(16.450Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.138826s(15.469Gflops)
Average Gflops: 16.878, Max Gflops: 18.160
Average Time: 0.127566s, Min Time: 0.118252s
The performance improvement is limited compared to C and Fortran, and it takes time to adjust the block size and try out the most appropriate parameters.
4. The Black Magic of Compilers
In the previous section, we have discussed the algorithm implementation using a simple loop and used some parallel libraries to accelerate the calculation. Now, we will not use parallel libraries but use the Fortran matmul function and the Rust ndarray and mathru libraries to implement matrix multiplication operations, to illustrate the importance of compiler optimization.
4.1 Fortran built-in function matmul
The content of main.f90 is consistent with that in 2.2. The content of the specific implementation file matmul.f90 is as follows.
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
c = matmul(a, b)
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
c = matmul(a, b)
end subroutine matrix_multiply_double
CMakeLists.txt removed openmp related code.
cmake_minimum_required(VERSION 3.13)
project(matmul-fortran LANGUAGES Fortran)
set(CMAKE_Fortran_STANDARD 2008)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_Fortran_COMPILER_FRONTEND_VARIANT}_${CMAKE_Fortran_COMPILER_ID}_${CMAKE_Fortran_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
set(SRC_LIST
src/main.f90
src/matmul.f90
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
)
Compiled using MSYS2’s ucrt64 toolchain under Windows, the Release program execution results are as follows:
PS D:\example\efficiency_v3\fortran\matmul-fortran\build> ."D:/example/efficiency_v3/fortran/matmul-fortran/build/matmul-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.049251s( 43.603Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.048811s( 43.996Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.048778s( 44.026Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.048698s( 44.098Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.046176s( 46.506Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.046269s( 46.413Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.046297s( 46.385Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.046634s( 46.049Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.046198s( 46.484Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.046255s( 46.428Gflops)
Average Gflops: 45.399, Max Gflops: 46.506
Average Time: 0.047337s, Min Time: 0.046176s
PS D:\example\efficiency_v3\fortran\matmul-fortran\build> ."D:/example/efficiency_v3/fortran/matmul-fortran/build/matmul-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.094482s( 22.729Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.093445s( 22.981Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.090847s( 23.638Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.089272s( 24.055Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.088472s( 24.273Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.088759s( 24.195Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.088489s( 24.268Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.088787s( 24.187Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.089572s( 23.975Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.088757s( 24.195Gflops)
Average Gflops: 23.850, Max Gflops: 24.273
Average Time: 0.090088s, Min Time: 0.088472s
Hyperthreading is not used, but it beats the combination of previous loop nesting and openmp methods. This may explain why C has been popular for decades but still cannot replace Fortran.
4.2 Rust implemented through the ndarray library
ndarray is a library used by Rust to process arrays, with a built-in matrix transposition function. Unlike the matrix stored in a one-dimensional array implemented in 2.3, using the ndarray library requires converting the one-dimensional array into a two-dimensional one.
The main.rs file is the same as in 2.3, and the matmul.rs file is as follows.
use ndarray::{Array2, ArrayView2};
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
let a = ArrayView2::from_shape((n, n), a).unwrap();
let b = ArrayView2::from_shape((n, n), b).unwrap();
let mut c_mat = Array2::<f32>::zeros((n, n));
c_mat.assign(&a.dot(&b));
c.copy_from_slice(c_mat.as_slice().unwrap());
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
let a = ArrayView2::from_shape((n, n), a).unwrap();
let b = ArrayView2::from_shape((n, n), b).unwrap();
let mut c_mat = Array2::<f64>::zeros((n, n));
c_mat.assign(&a.dot(&b));
c.copy_from_slice(c_mat.as_slice().unwrap());
}
The content of the Cargo.toml file is as follows.
[package]
name = "ndarray-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
ndarray = "0.16.1"
rand = "0.9.1"
Compiled using the msvc toolchain under Windows, the Release program has the following effects:
PS D:\example\efficiency_v3\rust\ndarray-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\ndarray-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.019414s(110.617Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.020280s(105.891Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.019639s(109.346Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.020076s(106.966Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.019702s(109.000Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.019438s(110.479Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.019336s(111.061Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.018605s(115.426Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.018340s(117.096Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.019040s(112.787Gflops)
Average Gflops: 110.867, Max Gflops: 117.096
Average Time: 0.019387s, Min Time: 0.018340s
PS D:\example\efficiency_v3\rust\ndarray-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\ndarray-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.041449s(51.811Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.039612s(54.213Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.039634s(54.183Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.040022s(53.657Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.038563s(55.687Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.037992s(56.524Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.038128s(56.324Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.038157s(56.280Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.038750s(55.419Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.038102s(56.361Gflops)
Average Gflops: 55.046, Max Gflops: 56.524
Average Time: 0.039041s, Min Time: 0.037992s
It also does not use hyperthreading, and it beats the previous loop nesting and rayon implementation combination. If the time difference caused by the conversion between one-dimensional arrays and two-dimensional arrays is not taken into account, the actual computing performance will actually be higher.
4.3 Rust implemented through the mathru library
Mathru is another Rust math library that provides many commonly used linear algebra calculation functions. The underlying algorithm can be implemented using Intel MKL or OpenBLAS.
Similarly, main.rs is not shown, and only the matmul.rs file is changed, as shown below.
use mathru::algebra::linear::matrix::General;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
let a_mat = General::new(n, n, a.to_vec());
let b_mat = General::new(n, n, b.to_vec());
let c_mat = &a_mat * &b_mat;
c.copy_from_slice(&c_mat.convert_to_vec());
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
let a_mat = General::new(n, n, a.to_vec());
let b_mat = General::new(n, n, b.to_vec());
let c_mat = a_mat * b_mat;
c.copy_from_slice(&c_mat.convert_to_vec());
}
The Cargo.toml file is as follows. The default implementation of mathru is used here, and Intel mkl or openblas is not used.
[package]
name = "mathru-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
mathru = "0.15.5"
rand = "0.9.1"
Compiled using the msvc toolchain under Windows, the Release program execution effect is as follows:
PS D:\example\efficiency_v3\rust\mathru-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.05s
Running `target\release\mathru-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.009277s(231.472Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.007753s(277.002Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.009030s(237.817Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.007585s(283.111Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.008559s(250.904Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.009235s(232.530Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.008425s(254.900Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.007451s(288.214Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.007609s(282.237Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.008545s(251.318Gflops)
Average Gflops: 258.950, Max Gflops: 288.214
Average Time: 0.008347s, Min Time: 0.007451s
PS D:\example\efficiency_v3\rust\mathru-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.05s
Running `target\release\mathru-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.016261s(132.063Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.016281s(131.904Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.015308s(140.282Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.016065s(133.672Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.016702s(128.578Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.014126s(152.019Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.017731s(121.116Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.020181s(106.409Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.015631s(137.388Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.015181s(141.459Gflops)
Average Gflops: 132.489, Max Gflops: 152.019
Average Time: 0.016347s, Min Time: 0.014126s
Without using multithreading, it is much faster than ndarray, which seems to indicate that some optimizations are done at the bottom layer. Similarly, if we do not consider the conversion between one-dimensional and two-dimensional arrays, the actual computing performance should be higher.
5. Summarize
C, Fortran and Rust matrix multiplication programs accelerated by parallel libraries such as OpenMP and Rayon use the same algorithm. The performance of matrix multiplication will be slightly different according to the implementation of different platforms and compilers, but generally they are in the same order of magnitude. This simple loop parallel acceleration calculation method is suitable for occasions with small matrix size. As the matrix size increases, the overall computing performance shows a decreasing trend.
Even if the block matrix + parallel library method is used to improve the cache hit rate, the performance improvement is still limited. Moreover, the matrix block size is related to the cache size of the computing platform, and a lot of tests are required to call out the appropriate block parameters.
The matrix multiplication function implemented using Fortran’s Matmul and Rust’s mathematical library, even without parallel acceleration, still leads the implementation of simple loop parallel acceleration in matrix multiplication performance. This just shows the importance of optimizing the underlying algorithm.
In the field of high-performance computing, in addition to the OpenMP parallel acceleration method, there are also BLAS, CUDA, MPI, etc., which will be further demonstrated in future articles.
