说到矩阵,只要是理工科都会想到被线性代数课支配的恐惧。矩阵乘法运算,往大了说各种工业和科研数值计算离不开它,往小了说各种跑分软件也会用到它,矩阵乘法运算的耗时也是评判计算机浮点运算性能的重要指标。本文的目的是通过矩阵乘法运算验证各种实现方式的性能差异,并对比不同计算平台的性能差异,为高性能计算开发提供参考。
1. 矩阵乘法算法
矩阵乘法运算也成为矩阵点乘,可以用下图表示1,通常由A矩阵对应行和B矩阵对应列的元素相乘并累加,形成C矩阵对应行列的值。要求A矩阵的列数要与B矩阵的行数相等,C矩阵的尺寸则相当于B矩阵的行数×A矩阵的列数。
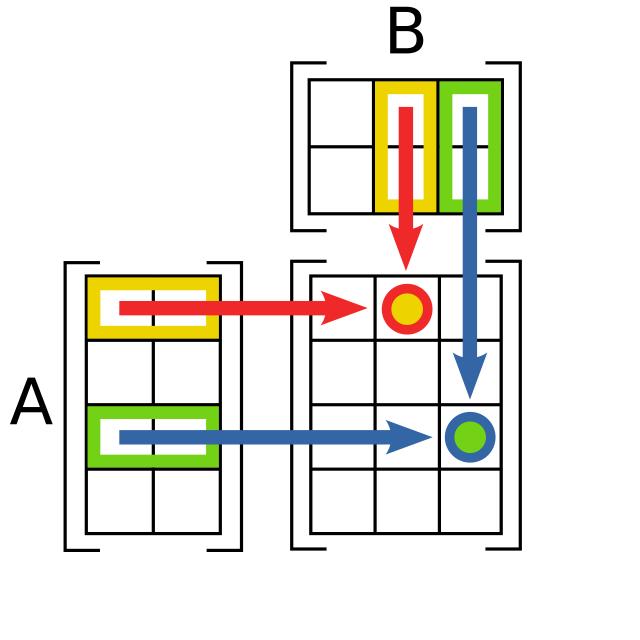
用C语言表示一个M×N矩阵点乘一个N×T矩阵,一般写成3层循环嵌套的形式。
...
for (int i = 0; i < M; i++)
{
for (int j = 0; j < T; j++)
{
C[i,j] = 0.0;
for (int k = 0; k < N; k++)
{
C[i,j] += A[i,k] * B[k,j];
}
}
}
...
通常认为一个N×N维矩阵的乘法次数为N的3次方,用O(n3)表示计算复杂度。也有一些算法,将其中某些乘法运算转化成加法,减少了乘法运算次数。比如Strassen算法2,理论上计算复杂度只有O(n2.807),降低了大矩阵相乘的耗时。更新的算法比如Coppersmith-Winograd方法,计算复杂度更是号称只有O(n2.3727)。这种算法上的差异不在本文讨论之列。
2. 循环嵌套并行化
现代计算机处理器一般都为多核心,为充分利用处理器性能,使用openmp等并行库对计算程序进行并行优化不失为一个好的选项。使用单核心进行循环嵌套求解没有实际意义,这里不做演示,有兴趣的可以在下面的代码中单独去掉并行库后进行编译计算。
2.1 C实现
C实现很简单,通过三层循环嵌套实现矩阵相乘算法。这里通过openmp将前两层循环合并分配到不同线程中展开计算3,以充分利用多核心处理器的性能。以下是openmp.c的示例代码。
#include <omp.h>
void matrix_multiply_float(int n, float A[], float B[], float C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
C[i * n + j] = 0;
for (int k = 0; k < n; k++)
{
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
void matrix_multiply_double(int n, double A[], double B[], double C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
C[i * n + j] = 0;
for (int k = 0; k < n; k++)
{
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
在main.c中定义一些命令行开关,用户可以自定义矩阵尺寸、循环次数、计算精度等。这里定义了一个性能参数,GFLOPs,用来衡量单位时间内执行浮点运算的能力,1GFLOPs相当于1秒内执行109次浮点运算。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <math.h>
#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define MIN(a, b) ((a) < (b) ? (a) : (b))
extern void matrix_multiply_float(int n, float A[], float B[], float C[]);
extern void matrix_multiply_double(int n, double A[], double B[], double C[]);
// Initialize matrix
void initialize_matrix_float(int n, float matrix[])
{
srand((unsigned)time(NULL));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
matrix[i * n + j] = rand() / (float)(RAND_MAX);
}
}
}
void initialize_matrix_double(int n, double matrix[])
{
srand((unsigned)time(NULL));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
matrix[i * n + j] = rand() / (double)(RAND_MAX);
}
}
}
// Execute matrix multiply and print results
int execute_float(int dim, int loop_num, double *ave_gflops, double *max_gflops, double *ave_time, double *min_time)
{
// Use volatile to prevent compiler optimizations
volatile float *a, *b, *c;
struct timespec start_ns, end_ns;
double cpu_time;
for (int i = 0; i < loop_num; i++)
{
a = (float *)malloc(dim * dim * sizeof(float));
b = (float *)malloc(dim * dim * sizeof(float));
c = (float *)malloc(dim * dim * sizeof(float));
if (a == NULL || b == NULL || c == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return 0;
}
initialize_matrix_float(dim, a);
initialize_matrix_float(dim, b);
timespec_get(&start_ns, TIME_UTC);
matrix_multiply_float(dim, a, b, c);
timespec_get(&end_ns, TIME_UTC);
cpu_time = (end_ns.tv_sec - start_ns.tv_sec) + (end_ns.tv_nsec - start_ns.tv_nsec) / 1e9;
double gflops = 1e-9 * dim * dim * dim * 2 / cpu_time;
printf("%d\t: %d x %d Matrix multiply wall time : %.6fs(%.3fGflops)\n", i + 1, dim, dim, cpu_time, gflops);
free(a);
free(b);
free(c);
*ave_gflops += gflops;
*max_gflops = MAX(*max_gflops, gflops);
*ave_time += cpu_time;
*min_time = MIN(*min_time, cpu_time);
}
*ave_gflops /= loop_num;
*ave_time /= loop_num;
return 1;
}
int execute_double(int dim, int loop_num, double *ave_gflops, double *max_gflops, double *ave_time, double *min_time)
{
// Use volatile to prevent compiler optimizations
volatile double *a, *b, *c;
struct timespec start_ns, end_ns;
double cpu_time;
for (int i = 0; i < loop_num; i++)
{
a = (double *)malloc(dim * dim * sizeof(double));
b = (double *)malloc(dim * dim * sizeof(double));
c = (double *)malloc(dim * dim * sizeof(double));
if (a == NULL || b == NULL || c == NULL)
{
fprintf(stderr, "Memory allocation failed\n");
return 0;
}
initialize_matrix_double(dim, a);
initialize_matrix_double(dim, b);
timespec_get(&start_ns, TIME_UTC);
matrix_multiply_double(dim, a, b, c);
timespec_get(&end_ns, TIME_UTC);
cpu_time = (end_ns.tv_sec - start_ns.tv_sec) + (end_ns.tv_nsec - start_ns.tv_nsec) / 1e9;
double gflops = 1e-9 * dim * dim * dim * 2 / cpu_time;
printf("%d\t: %d x %d Matrix multiply wall time : %.6fs(%.3fGflops)\n", i + 1, dim, dim, cpu_time, gflops);
free(a);
free(b);
free(c);
*ave_gflops += gflops;
*max_gflops = MAX(*max_gflops, gflops);
*ave_time += cpu_time;
*min_time = MIN(*min_time, cpu_time);
}
*ave_gflops /= loop_num;
*ave_time /= loop_num;
return 1;
}
int main(int argc, char *argv[])
{
int n = 10; // Default matrix size exponent
int loop_num = 5; // Number of iterations for averaging
double ave_gflops = 0.0, max_gflops = 0.0; // Average and maximum Gflops
double ave_time = 0.0, min_time = 1e9; // Average and minimum time
int use_double = 0; // Default to float precision
// Help message
if (argc == 1 || (argc == 2 && (strcmp(argv[1], "-h") == 0 || strcmp(argv[1], "--help") == 0)))
{
printf("Usage: %s [-n SIZE] [-l LOOP_NUM] [-float|-double]\n", argv[0]);
printf(" -n SIZE Specify matrix size, like 2^SIZE (default: 10)\n");
printf(" -l LOOP_NUM Specify number of iterations (default: 5)\n");
printf(" -float Use float precision (default)\n");
printf(" -double Use double precision\n");
printf(" -h, --help Show this help message\n");
return 0;
}
// Parse -n, -l, -float, -double options
int double_flag = 0, float_flag = 0;
for (int argi = 1; argi < argc; ++argi)
{
if (strcmp(argv[argi], "-n") == 0 && argi + 1 < argc)
{
n = atoi(argv[argi + 1]);
argi++;
}
else if (strcmp(argv[argi], "-l") == 0 && argi + 1 < argc)
{
loop_num = atoi(argv[argi + 1]);
argi++;
}
else if (strcmp(argv[argi], "-double") == 0)
{
double_flag = 1;
}
else if (strcmp(argv[argi], "-float") == 0)
{
float_flag = 1;
}
}
if (double_flag && float_flag)
{
fprintf(stderr, "Error: Cannot specify both -double and -float options.\n");
return 1;
}
use_double = double_flag ? 1 : 0;
int dim = (int)pow(2, n);
if (use_double)
{
printf("Using double precision for matrix multiplication.\n");
execute_double(dim, loop_num, &ave_gflops, &max_gflops, &ave_time, &min_time);
}
else
{
printf("Using float precision for matrix multiplication.\n");
execute_float(dim, loop_num, &ave_gflops, &max_gflops, &ave_time, &min_time);
}
printf("Average Gflops: %.3f, Max Gflops: %.3f\n", ave_gflops, max_gflops);
printf("Average Time: %.6fs, Min Time: %.6fs\n", ave_time, min_time);
return 0;
}
这里用到了cmake,CMakeLists.txt告诉编译器怎么包含openmp的头文件并链接到它。
cmake_minimum_required(VERSION 3.13)
project(openmp LANGUAGES C)
set(CMAKE_C_STANDARD 11)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_C_COMPILER_FRONTEND_VARIANT}_${CMAKE_C_COMPILER_ID}_${CMAKE_C_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
find_package(OpenMP REQUIRED)
set(SRC_LIST
src/main.c
src/openmp.c
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
OpenMP::OpenMP_C
)
Windows下使用vs2022的clang-cl编译出来的Release程序,执行效果如下:
PS D:\example\efficiency_v3\c\openmp\build\Release> ."D:/example/efficiency_v3/c/openmp/build/Release/openmp_msvc_clang_19.1.5.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.362688s(5.921Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.304758s(7.047Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.314348s(6.832Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.294248s(7.298Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.294496s(7.292Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.306986s(6.995Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.320405s(6.702Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.278521s(7.710Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.294080s(7.302Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.338626s(6.342Gflops)
Average Gflops: 6.944, Max Gflops: 7.710
Average Time: 0.310916s, Min Time: 0.278521s
PS D:\example\efficiency_v3\c\openmp\build\Release> ."D:/example/efficiency_v3/c/openmp/build/Release/openmp_msvc_clang_19.1.5.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.353909s(6.068Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.319001s(6.732Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.329514s(6.517Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.381114s(5.635Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.349447s(6.145Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.370087s(5.803Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.349626s(6.142Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.370023s(5.804Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.364005s(5.900Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.344441s(6.235Gflops)
Average Gflops: 6.098, Max Gflops: 6.732
Average Time: 0.353117s, Min Time: 0.319001s
使用MSYS2的clang64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_clang_20.1.7.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.344437s(6.235Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.327010s(6.567Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.367141s(5.849Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.358603s(5.988Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.362182s(5.929Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.338947s(6.336Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.334758s(6.415Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.331219s(6.484Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.343316s(6.255Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.324451s(6.619Gflops)
Average Gflops: 6.268, Max Gflops: 6.619
Average Time: 0.343206s, Min Time: 0.324451s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_clang_20.1.7.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.447118s(4.803Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.423630s(5.069Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.365229s(5.880Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.355163s(6.046Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.443296s(4.844Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.310319s(6.920Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.366405s(5.861Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.369704s(5.809Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.382898s(5.608Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.367266s(5.847Gflops)
Average Gflops: 5.669, Max Gflops: 6.920
Average Time: 0.383103s, Min Time: 0.310319s
切换成MSYS2的ucrt64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.308967s(6.951Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.267709s(8.022Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.278587s(7.708Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.263047s(8.164Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.262595s(8.178Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.264196s(8.128Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.273148s(7.862Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.262910s(8.168Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.277290s(7.745Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.274961s(7.810Gflops)
Average Gflops: 7.874, Max Gflops: 8.178
Average Time: 0.273341s, Min Time: 0.262595s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.314685s(6.824Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.290665s(7.388Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.304162s(7.060Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.315041s(6.817Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.306290s(7.011Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.356495s(6.024Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.310081s(6.926Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.301022s(7.134Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.317229s(6.769Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.307106s(6.993Gflops)
Average Gflops: 6.895, Max Gflops: 7.388
Average Time: 0.312278s, Min Time: 0.290665s
Windows下gcc编译器的表现要好一点,三者运算性能基本都在同一量级,差异比较小可以忽略不记。
以上均是在AMD AI 9 365w处理器计算的结果,计算过程中基本跑满了所有核心和超线程。本文展示的计算结果,如果没有特殊说明,都是在该处理器上运行输出的结果。
2.2 fortran实现
fortran有内置的矩阵运算函数matmul,这里先不考虑内置函数的算法优化。将C实现的3层循环嵌套用Fortran实现,再通过openmp加速。
main.f90实现功能和C实现的main.c一致。
program main
implicit none
external matrix_multiply_float, matrix_multiply_double
integer :: n = 10
integer :: loop_num = 5
real :: ave_gflops = 0.0, max_gflops = 0.0
real :: ave_time = 0.0, min_time = 1e9
logical :: use_double = .false.
integer :: argi, i, dim
character(len=100) :: arg
logical :: double_set = .false., float_set = .false.
if (command_argument_count() == 0) then
call print_help()
stop
end if
argi = 1
do while (argi <= command_argument_count())
call get_command_argument(argi, arg)
if (trim(arg) == '-n' .and. argi + 1 <= command_argument_count()) then
argi = argi + 1
call get_command_argument(argi, arg)
read(arg, *) n
else if (trim(arg) == '-l' .and. argi + 1 <= command_argument_count()) then
argi = argi + 1
call get_command_argument(argi, arg)
read(arg, *) loop_num
else if (trim(arg) == '-double') then
double_set = .true.
use_double = .true.
else if (trim(arg) == '-float') then
float_set = .true.
use_double = .false.
else if (trim(arg) == '-h' .or. trim(arg) == '--help') then
call print_help()
stop
end if
if (double_set .and. float_set) then
print *, "Error: Cannot specify both -double and -float options."
stop
end if
argi = argi + 1
end do
dim = 2**n
if (use_double) then
call perform_double(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
else
call perform_float(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
end if
ave_gflops = ave_gflops / loop_num
ave_time = ave_time / loop_num
print '(A, F8.3, A, F8.3)', 'Average Gflops: ', ave_gflops, ', Max Gflops: ', max_gflops
print '(A, F10.6, A, F10.6, A)', 'Average Time: ', ave_time, 's, Min Time: ', min_time, 's'
contains
subroutine print_help()
print *, 'Usage: program_name [-n SIZE] [-l LOOP_NUM] [-float|-double]'
print *, ' -n SIZE Specify matrix size, like 2^SIZE (default: 10)'
print *, ' -l LOOP_NUM Specify number of iterations (default: 5)'
print *, ' -float Use real*32 precision (default)'
print *, ' -double Use real*64 precision'
print *, ' -h, --help Show this help message'
end subroutine print_help
subroutine initialize_matrix_float(n, matrix)
integer, intent(in) :: n
real, intent(out) :: matrix(n, n)
integer :: i, j
real :: rand
call random_seed()
do i = 1, n
do j = 1, n
call random_number(rand)
matrix(i, j) = rand
end do
end do
end subroutine initialize_matrix_float
subroutine initialize_matrix_double(n, matrix)
integer, intent(in) :: n
real*8, intent(out) :: matrix(n, n)
integer :: i, j
real*8 :: rand
call random_seed()
do i = 1, n
do j = 1, n
call random_number(rand)
matrix(i, j) = rand
end do
end do
end subroutine initialize_matrix_double
subroutine perform_double(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
integer, intent(in) :: dim, loop_num
real, intent(inout) :: ave_gflops, max_gflops, ave_time
real, intent(inout) :: min_time
real*8, allocatable :: a_double(:, :), b_double(:, :), c_double(:, :)
real :: gflops
integer*8 :: i, start_count(1), end_count(1), count_rate(1)
real :: elapsed_time
print *, 'Using real*64 precision for matrix multiplication.'
allocate(a_double(dim, dim), b_double(dim, dim), c_double(dim, dim))
do i = 1, loop_num
call initialize_matrix_double(dim, a_double)
call initialize_matrix_double(dim, b_double)
call system_clock(count=start_count(1), count_rate=count_rate(1))
call matrix_multiply_double(dim, a_double, b_double, c_double)
call system_clock(count=end_count(1))
elapsed_time = real(end_count(1) - start_count(1)) / real(count_rate(1))
gflops = 1e-9 * dim * dim * dim * 2 / elapsed_time
print '(I8, A, I0, A, I0, A, F10.6, A, F8.3, A)', i, ' : ', dim, ' x ', dim, ' Matrix multiply wall time : ', elapsed_time, 's(', gflops, 'Gflops)'
ave_gflops = ave_gflops + gflops
max_gflops = max(max_gflops, gflops)
ave_time = ave_time + elapsed_time
min_time = min(min_time, elapsed_time)
end do
deallocate(a_double, b_double, c_double)
end subroutine perform_double
subroutine perform_float(dim, loop_num, ave_gflops, max_gflops, ave_time, min_time)
integer, intent(in) :: dim, loop_num
real, intent(inout) :: ave_gflops, max_gflops, ave_time
real, intent(inout) :: min_time
real*4, allocatable :: a_float(:, :), b_float(:, :), c_float(:, :)
real :: gflops
integer*8 :: i, start_count(1), end_count(1), count_rate(1)
real :: elapsed_time
print *, 'Using real*32 precision for matrix multiplication.'
allocate(a_float(dim, dim), b_float(dim, dim), c_float(dim, dim))
do i = 1, loop_num
call initialize_matrix_float(dim, a_float)
call initialize_matrix_float(dim, b_float)
call system_clock(count=start_count(1), count_rate=count_rate(1))
call matrix_multiply_float(dim, a_float, b_float, c_float)
call system_clock(count=end_count(1))
elapsed_time = real(end_count(1) - start_count(1)) / real(count_rate(1))
gflops = 1e-9 * dim * dim * dim * 2 / elapsed_time
print '(I8, A, I0, A, I0, A, F10.6, A, F8.3, A)', i, ' : ', dim, ' x ', dim, ' Matrix multiply wall time : ', elapsed_time, 's(', gflops, 'Gflops)'
ave_gflops = ave_gflops + gflops
max_gflops = max(max_gflops, gflops)
ave_time = ave_time + elapsed_time
min_time = min(min_time, elapsed_time)
end do
deallocate(a_float, b_float, c_float)
end subroutine perform_float
end program main
omp.f90是3层循环算法的具体实现,同样用openmp展开前两层循环实现并行化。
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer, intent(in) :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
integer :: i, j, k
c = 0.0
!$omp parallel do private(i, j, k) shared(a, b, c, n) collapse(2)
do i = 1, n
do j = 1, n
do k = 1, n
c(i, j) = c(i, j) + a(i, k) * b(k, j)
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer, intent(in) :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
integer :: i, j, k
c = 0.0d0
!$omp parallel do private(i, j, k) shared(a, b, c, n) collapse(2)
do i = 1, n
do j = 1, n
do k = 1, n
c(i, j) = c(i, j) + a(i, k) * b(k, j)
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_double
CMakeLists.txt文件如下:
cmake_minimum_required(VERSION 3.13)
project(openmp-fortran LANGUAGES Fortran)
set(CMAKE_Fortran_STANDARD 2008)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_Fortran_COMPILER_FRONTEND_VARIANT}_${CMAKE_Fortran_COMPILER_ID}_${CMAKE_Fortran_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
# Enable OpenMP
find_package(OpenMP REQUIRED)
set(SRC_LIST
src/main.f90
src/omp.f90
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
OpenMP::OpenMP_Fortran
)
使用Intel oneAPI的ifx编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build\Release> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/Release/openmp-fortran_msvc_intelllvm_2025.1.1.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.299000s( 7.182Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.284000s( 7.562Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.337000s( 6.372Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.310000s( 6.927Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.321000s( 6.690Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.358000s( 5.999Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.290000s( 7.405Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.312000s( 6.883Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.301000s( 7.134Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.290000s( 7.405Gflops)
Average Gflops: 6.956, Max Gflops: 7.562
Average Time: 0.310200s, Min Time: 0.284000s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build\Release> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/Release/openmp-fortran_msvc_intelllvm_2025.1.1.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.391000s( 5.492Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.362000s( 5.932Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.334000s( 6.430Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.393000s( 5.464Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.331000s( 6.488Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.357000s( 6.015Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.366000s( 5.867Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.345000s( 6.225Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.341000s( 6.298Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.359000s( 5.982Gflops)
Average Gflops: 6.019, Max Gflops: 6.488
Average Time: 0.357900s, Min Time: 0.331000s
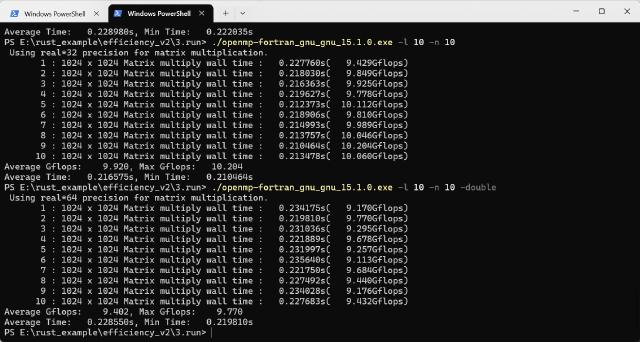
使用MSYS2的ucrt64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.224624s( 9.560Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.224959s( 9.546Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.228968s( 9.379Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.238853s( 8.991Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.216879s( 9.902Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.212407s( 10.110Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.233809s( 9.185Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.240426s( 8.932Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.241291s( 8.900Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.222414s( 9.655Gflops)
Average Gflops: 9.416, Max Gflops: 10.110
Average Time: 0.228463s, Min Time: 0.212407s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.258885s( 8.295Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.299699s( 7.165Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.298025s( 7.206Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.291631s( 7.364Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.271050s( 7.923Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.330989s( 6.488Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.278846s( 7.701Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.281121s( 7.639Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.288999s( 7.431Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.318669s( 6.739Gflops)
Average Gflops: 7.395, Max Gflops: 8.295
Average Time: 0.291792s, Min Time: 0.258885s
在AMD处理器上运行的结果,Intel ifx版本比gcc版本要慢一些,多次尝试也是如此。
将生成的程序拷贝到Intel工作站(Xeon Gold 6226R)上运行,两者运行时间基本相同。很令人怀疑是不是Intel的编译器针对AMD平台做了某些负优化。

2.3 rust实现
rust下没有openmp原生实现,但有类似功能的并行库rayon,这里用rust+rayon实现3层循环嵌套算法。
main.rs实现和main.c相同的功能。
mod matmul;
use matmul::{matrix_multiply_double, matrix_multiply_float};
use clap::{Arg, ArgAction, Command};
use rand::prelude::*;
use std::time::Instant;
fn initialize_matrix_float(n: usize, matrix: &mut [f32]) {
let mut rng = rand::rng();
for i in 0..n * n {
matrix[i] = rng.random::<f32>();
}
}
fn initialize_matrix_double(n: usize, matrix: &mut [f64]) {
let mut rng = rand::rng();
for i in 0..n * n {
matrix[i] = rng.random::<f64>();
}
}
fn execute_float(dim: usize, loop_num: usize) -> (f64, f64, f64, f64) {
let mut ave_gflops: f64 = 0.0;
let mut max_gflops: f64 = 0.0;
let mut ave_time: f64 = 0.0;
let mut min_time = f64::MAX;
for i in 0..loop_num {
let mut a = vec![0.0; dim * dim];
let mut b = vec![0.0; dim * dim];
let mut c = vec![0.0; dim * dim];
initialize_matrix_float(dim, &mut a);
initialize_matrix_float(dim, &mut b);
let start = Instant::now();
matrix_multiply_float(dim, &a, &b, &mut c);
let cpu_time = start.elapsed().as_secs_f64();
let gflops = 2.0 * (dim * dim * dim) as f64 / cpu_time / 1e9;
println!(
"{}\t: {} x {} Matrix multiply wall time : {:.6}s({:.3}Gflops)",
i + 1,
dim,
dim,
cpu_time,
gflops
);
ave_gflops += gflops;
max_gflops = max_gflops.max(gflops);
ave_time += cpu_time;
min_time = min_time.min(cpu_time);
}
ave_gflops /= loop_num as f64;
ave_time /= loop_num as f64;
(ave_gflops, max_gflops, ave_time, min_time)
}
fn execute_double(dim: usize, loop_num: usize) -> (f64, f64, f64, f64) {
let mut ave_gflops: f64 = 0.0;
let mut max_gflops: f64 = 0.0;
let mut ave_time: f64 = 0.0;
let mut min_time = f64::MAX;
for i in 0..loop_num {
let mut a = vec![0.0; dim * dim];
let mut b = vec![0.0; dim * dim];
let mut c = vec![0.0; dim * dim];
initialize_matrix_double(dim, &mut a);
initialize_matrix_double(dim, &mut b);
let start = Instant::now();
matrix_multiply_double(dim, &a, &b, &mut c);
let cpu_time = start.elapsed().as_secs_f64();
let gflops = 2.0 * (dim * dim * dim) as f64 / cpu_time / 1e9;
println!(
"{}\t: {} x {} Matrix multiply wall time : {:.6}s({:.3}Gflops)",
i + 1,
dim,
dim,
cpu_time,
gflops
);
ave_gflops += gflops;
max_gflops = max_gflops.max(gflops);
ave_time += cpu_time;
min_time = min_time.min(cpu_time);
}
ave_gflops /= loop_num as f64;
ave_time /= loop_num as f64;
(ave_gflops, max_gflops, ave_time, min_time)
}
fn main() {
let matches = Command::new("rayon-rs")
.version("0.1.0")
.author("AndrewMoa")
.about("Matrix multiplication benchmark")
.arg(
Arg::new("size")
.short('n')
.long("size")
.help("Matrix size exponent (size = 2^n)")
.default_value("10"),
)
.arg(
Arg::new("loops")
.short('l')
.long("loops")
.help("Number of iterations")
.default_value("5"),
)
.arg(
Arg::new("f64")
.short('d')
.long("f64")
.help("Use float64 precision")
.action(ArgAction::SetTrue),
)
.arg(
Arg::new("f32")
.short('f')
.long("f32")
.help("Use float32 precision (default)")
.action(ArgAction::SetTrue),
)
.get_matches();
let n: usize = matches
.get_one::<String>("size")
.unwrap()
.parse()
.expect("Invalid size exponent");
let loop_num: usize = matches
.get_one::<String>("loops")
.unwrap()
.parse()
.expect("Invalid loop count");
let use_double = matches.get_flag("f64");
let use_float = matches.get_flag("f32");
if use_double && use_float {
eprintln!("Error: Cannot specify both --f64 and --f32");
std::process::exit(1);
}
let dim = 2usize.pow(n as u32);
if use_double {
println!("Using f64 precision for matrix multiplication.");
let (ave_gflops, max_gflops, ave_time, min_time) = execute_double(dim, loop_num);
println!(
"Average Gflops: {:.3}, Max Gflops: {:.3}",
ave_gflops, max_gflops
);
println!("Average Time: {:.6}s, Min Time: {:.6}s", ave_time, min_time);
} else {
println!("Using f32 precision for matrix multiplication.");
let (ave_gflops, max_gflops, ave_time, min_time) = execute_float(dim, loop_num);
println!(
"Average Gflops: {:.3}, Max Gflops: {:.3}",
ave_gflops, max_gflops
);
println!("Average Time: {:.6}s, Min Time: {:.6}s", ave_time, min_time);
}
}
matmul.rs实现具体算法,这里用2层循环代替了3层循环,再通过rayon展开最外层循环实现并行化,实际效果和openmp是类似的。
use rayon::prelude::*;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
c.par_iter_mut().enumerate().for_each(|(idx, c_ij)| {
let i = idx / n;
let j = idx % n;
*c_ij = 0.0;
for k in 0..n {
*c_ij += a[i * n + k] * b[k * n + j];
}
});
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
c.par_iter_mut().enumerate().for_each(|(idx, c_ij)| {
let i = idx / n;
let j = idx % n;
*c_ij = 0.0;
for k in 0..n {
*c_ij += a[i * n + k] * b[k * n + j];
}
});
}
Cargo.toml文件如下所示。
[package]
name = "rayon-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
rand = "0.9.1"
rayon = "1.10.0"
Windows下使用msvc工具链编译,Release程序效果如下:
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\rayon-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.183645s(11.694Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.189942s(11.306Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.186613s(11.508Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.190823s(11.254Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.197830s(10.855Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.194282s(11.053Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.199380s(10.771Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.198576s(10.814Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.190201s(11.291Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.195518s(10.984Gflops)
Average Gflops: 11.153, Max Gflops: 11.694
Average Time: 0.192681s, Min Time: 0.183645s
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\rayon-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.188721s(11.379Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.186753s(11.499Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.206919s(10.378Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.197388s(10.879Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.196899s(10.907Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.206537s(10.398Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.200781s(10.696Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.191448s(11.217Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.192770s(11.140Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.178019s(12.063Gflops)
Average Gflops: 11.056, Max Gflops: 12.063
Average Time: 0.194624s, Min Time: 0.178019s
3. 分块矩阵并行化
直接求解大矩阵时,为提高求解效率,可以将大矩阵分割为小块进行求解,这样可以提高缓存命中率,一定程度上可以提高计算性能。
3.1 分块矩阵C实现
在2.1实现的基础上更改openmp.c文件内容如下,其他文件内容保持不变。
#include <omp.h>
#include <math.h>
// 分块大小,根据缓存大小调整
#define BLOCK_SIZE 8
void matrix_multiply_float(int n, float A[], float B[], float C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i_block = 0; i_block < n; i_block += BLOCK_SIZE) {
for (int j_block = 0; j_block < n; j_block += BLOCK_SIZE) {
for (int k_block = 0; k_block < n; k_block += BLOCK_SIZE) {
int i_end = fmin(i_block + BLOCK_SIZE, n);
int j_end = fmin(j_block + BLOCK_SIZE, n);
int k_end = fmin(k_block + BLOCK_SIZE, n);
for (int i = i_block; i < i_end; i++) {
for (int j = j_block; j < j_end; j++) {
for (int k = k_block; k < k_end; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
}
}
}
void matrix_multiply_double(int n, double A[], double B[], double C[])
{
#pragma omp parallel for collapse(2) shared(A, B, C)
for (int i_block = 0; i_block < n; i_block += BLOCK_SIZE) {
for (int j_block = 0; j_block < n; j_block += BLOCK_SIZE) {
for (int k_block = 0; k_block < n; k_block += BLOCK_SIZE) {
int i_end = fmin(i_block + BLOCK_SIZE, n);
int j_end = fmin(j_block + BLOCK_SIZE, n);
int k_end = fmin(k_block + BLOCK_SIZE, n);
for (int i = i_block; i < i_end; i++) {
for (int j = j_block; j < j_end; j++) {
for (int k = k_block; k < k_end; k++) {
C[i * n + j] += A[i * n + k] * B[k * n + j];
}
}
}
}
}
}
}
Windows下使用MSYS2的ucrt64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using float precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.058133s(36.941Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.060944s(35.237Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.060845s(35.294Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.060216s(35.663Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.061135s(35.127Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.060427s(35.539Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.059523s(36.078Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.060110s(35.726Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.062199s(34.526Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.059708s(35.966Gflops)
Average Gflops: 35.610, Max Gflops: 36.941
Average Time: 0.060324s, Min Time: 0.058133s
PS D:\example\efficiency_v3\c\openmp\build> ."D:/example/efficiency_v3/c/openmp/build/openmp_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using double precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.065988s(32.544Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.056852s(37.773Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.059504s(36.090Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.053153s(40.402Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.057459s(37.374Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.053974s(39.787Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.055030s(39.024Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.053222s(40.349Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.054025s(39.750Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.053405s(40.211Gflops)
Average Gflops: 38.330, Max Gflops: 40.402
Average Time: 0.056261s, Min Time: 0.053153s
相比于循环嵌套算法,分块之后性能有了很大的提升。分块大小和硬件平台有关,直接影响缓存命中率,进而影响计算性能,需要通过大量测试才能确定分块大小在多少最为合适。
3.2 分块矩阵fortran实现
在2.2内容的基础上,仅仅变更omp.f90文件,增加分块矩阵算法。
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer, intent(in) :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
integer :: i, j, k, bi, bj, bk, block_size
real*4 :: temp
! 定义块大小,根据缓存情况调整
block_size = 8
c = 0.0
!$omp parallel do private(bi, bj, bk, i, j, k, temp) shared(a, b, c, n, block_size)
do bi = 1, n, block_size
do bj = 1, n, block_size
do bk = 1, n, block_size
do i = bi, min(bi + block_size - 1, n)
do j = bj, min(bj + block_size - 1, n)
temp = c(i, j)
do k = bk, min(bk + block_size - 1, n)
temp = temp + a(i, k) * b(k, j)
end do
c(i, j) = temp
end do
end do
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer, intent(in) :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
integer :: i, j, k, bi, bj, bk, block_size
real*8 :: temp
block_size = 8
c = 0.0d0
!$omp parallel do private(bi, bj, bk, i, j, k, temp) shared(a, b, c, n, block_size)
do bi = 1, n, block_size
do bj = 1, n, block_size
do bk = 1, n, block_size
do i = bi, min(bi + block_size - 1, n)
do j = bj, min(bj + block_size - 1, n)
temp = c(i, j)
do k = bk, min(bk + block_size - 1, n)
temp = temp + a(i, k) * b(k, j)
end do
c(i, j) = temp
end do
end do
end do
end do
end do
!$omp end parallel do
end subroutine matrix_multiply_double
Windows下使用MSYS2的ucrt64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.091248s( 23.535Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.082953s( 25.888Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.080934s( 26.534Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.078231s( 27.451Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.076461s( 28.086Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.078698s( 27.288Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.077900s( 27.567Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.079131s( 27.138Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.083838s( 25.615Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.078336s( 27.414Gflops)
Average Gflops: 26.651, Max Gflops: 28.086
Average Time: 0.080773s, Min Time: 0.076461s
PS D:\example\efficiency_v3\fortran\openmp-fortran\build> ."D:/example/efficiency_v3/fortran/openmp-fortran/build/openmp-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.087275s( 24.606Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.080483s( 26.682Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.079304s( 27.079Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.080373s( 26.719Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.076651s( 28.016Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.080497s( 26.678Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.097153s( 22.104Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.085253s( 25.190Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.085751s( 25.043Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.098205s( 21.867Gflops)
Average Gflops: 25.399, Max Gflops: 28.016
Average Time: 0.085094s, Min Time: 0.076651s
性能提升取决于分块大小,可以通过调整分块大小慢慢试出最合适的参数。
3.3 分块矩阵rust实现
同样地,在2.3的基础上,这里仅仅改动matmul.rs文件。
use rayon::prelude::*;
// 定义分块大小
const BLOCK_SIZE: usize = 8;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
c.par_chunks_mut(n).enumerate().for_each(|(i, c_row)| {
for bj in (0..n).step_by(BLOCK_SIZE) {
for bk in (0..n).step_by(BLOCK_SIZE) {
for j in bj..(bj + BLOCK_SIZE).min(n) {
for k in bk..(bk + BLOCK_SIZE).min(n) {
c_row[j] += a[i * n + k] * b[k * n + j];
}
}
}
}
});
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
c.par_chunks_mut(n).enumerate().for_each(|(i, c_row)| {
for bj in (0..n).step_by(BLOCK_SIZE) {
for bk in (0..n).step_by(BLOCK_SIZE) {
for j in bj..(bj + BLOCK_SIZE).min(n) {
for k in bk..(bk + BLOCK_SIZE).min(n) {
c_row[j] += a[i * n + k] * b[k * n + j];
}
}
}
}
});
}
Windows下使用msvc工具链编译,Release程序效果如下:
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.03s
Running `target\release\rayon-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.113868s(18.859Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.116698s(18.402Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.125060s(17.172Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.125669s(17.088Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.116527s(18.429Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.114784s(18.709Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.117369s(18.297Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.114227s(18.800Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.118140s(18.177Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.115756s(18.552Gflops)
Average Gflops: 18.249, Max Gflops: 18.859
Average Time: 0.117810s, Min Time: 0.113868s
PS D:\example\efficiency_v3\rust\rayon-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.03s
Running `target\release\rayon-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.120614s(17.805Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.128292s(16.739Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.122600s(17.516Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.118252s(18.160Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.127342s(16.864Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.121794s(17.632Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.130288s(16.483Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.137106s(15.663Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.130548s(16.450Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.138826s(15.469Gflops)
Average Gflops: 16.878, Max Gflops: 18.160
Average Time: 0.127566s, Min Time: 0.118252s
提升幅度相比C和fortran比较有限,需要时间调整分块大小试出最合适的参数。
4. 编译器黑魔法
前面讲了简单的循环实现算法,并且用了一些并行库实现计算加速。下面不使用并行库,改用fortran的matmul函数、以及rust的ndarray库和mathru库实现矩阵乘法运算,说明编译器优化的重要性。
4.1 fortran内置函数matmul
main.f90和2.2中的内容一致,具体实现的matmul.f90文件内容如下。
subroutine matrix_multiply_float(n, a, b, c)
implicit none
integer :: n
real*4, intent(in) :: a(n, n), b(n, n)
real*4, intent(out) :: c(n, n)
c = matmul(a, b)
end subroutine matrix_multiply_float
subroutine matrix_multiply_double(n, a, b, c)
implicit none
integer :: n
real*8, intent(in) :: a(n, n), b(n, n)
real*8, intent(out) :: c(n, n)
c = matmul(a, b)
end subroutine matrix_multiply_double
CMakeLists.txt移除了openmp相关代码。
cmake_minimum_required(VERSION 3.13)
project(matmul-fortran LANGUAGES Fortran)
set(CMAKE_Fortran_STANDARD 2008)
set(EXECUTE_FILE_NAME ${PROJECT_NAME}_${CMAKE_Fortran_COMPILER_FRONTEND_VARIANT}_${CMAKE_Fortran_COMPILER_ID}_${CMAKE_Fortran_COMPILER_VERSION})
string(TOLOWER ${EXECUTE_FILE_NAME} EXECUTE_FILE_NAME)
set(SRC_LIST
src/main.f90
src/matmul.f90
)
add_executable(${EXECUTE_FILE_NAME} ${SRC_LIST})
target_link_libraries(${EXECUTE_FILE_NAME} PRIVATE
)
Windows下使用MSYS2的ucrt64工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\fortran\matmul-fortran\build> ."D:/example/efficiency_v3/fortran/matmul-fortran/build/matmul-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10
Using real*32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.049251s( 43.603Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.048811s( 43.996Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.048778s( 44.026Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.048698s( 44.098Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.046176s( 46.506Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.046269s( 46.413Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.046297s( 46.385Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.046634s( 46.049Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.046198s( 46.484Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.046255s( 46.428Gflops)
Average Gflops: 45.399, Max Gflops: 46.506
Average Time: 0.047337s, Min Time: 0.046176s
PS D:\example\efficiency_v3\fortran\matmul-fortran\build> ."D:/example/efficiency_v3/fortran/matmul-fortran/build/matmul-fortran_gnu_gnu_15.1.0.exe" -l 10 -n 10 -double
Using real*64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.094482s( 22.729Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.093445s( 22.981Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.090847s( 23.638Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.089272s( 24.055Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.088472s( 24.273Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.088759s( 24.195Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.088489s( 24.268Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.088787s( 24.187Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.089572s( 23.975Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.088757s( 24.195Gflops)
Average Gflops: 23.850, Max Gflops: 24.273
Average Time: 0.090088s, Min Time: 0.088472s
没有用到超线程,但吊打前面的循环嵌套+openmp方法,这也许能解释为什么C火了几十年但仍旧取代不了fortran。
4.2 rust通过ndarray库实现
ndarray是rust用于处理数组的库,内置了矩阵转置函数。与2.3中实现的通过一维数组存储的矩阵不同,使用ndarray库需要将一维数组转换成二维。
main.rs文件同2.3中的一致,matmul.rs文件如下所示。
use ndarray::{Array2, ArrayView2};
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
let a = ArrayView2::from_shape((n, n), a).unwrap();
let b = ArrayView2::from_shape((n, n), b).unwrap();
let mut c_mat = Array2::<f32>::zeros((n, n));
c_mat.assign(&a.dot(&b));
c.copy_from_slice(c_mat.as_slice().unwrap());
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
let a = ArrayView2::from_shape((n, n), a).unwrap();
let b = ArrayView2::from_shape((n, n), b).unwrap();
let mut c_mat = Array2::<f64>::zeros((n, n));
c_mat.assign(&a.dot(&b));
c.copy_from_slice(c_mat.as_slice().unwrap());
}
Cargo.toml文件如下所示。
[package]
name = "ndarray-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
ndarray = "0.16.1"
rand = "0.9.1"
Windows下使用msvc工具链编译,Release程序效果如下:
PS D:\example\efficiency_v3\rust\ndarray-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\ndarray-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.019414s(110.617Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.020280s(105.891Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.019639s(109.346Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.020076s(106.966Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.019702s(109.000Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.019438s(110.479Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.019336s(111.061Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.018605s(115.426Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.018340s(117.096Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.019040s(112.787Gflops)
Average Gflops: 110.867, Max Gflops: 117.096
Average Time: 0.019387s, Min Time: 0.018340s
PS D:\example\efficiency_v3\rust\ndarray-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.04s
Running `target\release\ndarray-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.041449s(51.811Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.039612s(54.213Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.039634s(54.183Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.040022s(53.657Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.038563s(55.687Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.037992s(56.524Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.038128s(56.324Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.038157s(56.280Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.038750s(55.419Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.038102s(56.361Gflops)
Average Gflops: 55.046, Max Gflops: 56.524
Average Time: 0.039041s, Min Time: 0.037992s
同样没有用到超线程,吊打前面的循环嵌套+rayon实现。如果不考虑一维数组和二维数组之间转换所带来的时间差,实际计算性能其实只会更高。
4.3 rust通过mathru库实现
mathru是另一个rust数学库,提供了很多常用的线性代数计算函数,底层算法可以选择采用intel mkl或者openblas实现。
同样地main.rs不表,只更改matmul.rs文件,如下所示。
use mathru::algebra::linear::matrix::General;
pub fn matrix_multiply_float(n: usize, a: &[f32], b: &[f32], c: &mut [f32]) {
let a_mat = General::new(n, n, a.to_vec());
let b_mat = General::new(n, n, b.to_vec());
let c_mat = &a_mat * &b_mat;
c.copy_from_slice(&c_mat.convert_to_vec());
}
pub fn matrix_multiply_double(n: usize, a: &[f64], b: &[f64], c: &mut [f64]) {
let a_mat = General::new(n, n, a.to_vec());
let b_mat = General::new(n, n, b.to_vec());
let c_mat = a_mat * b_mat;
c.copy_from_slice(&c_mat.convert_to_vec());
}
Cargo.toml文件如下所示,这里使用mathru的默认实现,没有使用intel mkl或者openblas。
[package]
name = "mathru-rs"
version = "0.1.0"
edition = "2024"
[dependencies]
clap = { version = "4.5.40", features = ["derive"] }
mathru = "0.15.5"
rand = "0.9.1"
Windows下使用msvc工具链编译,Release程序执行效果如下:
PS D:\example\efficiency_v3\rust\mathru-rs> cargo run --release -- -l 10 -n 10
Finished `release` profile [optimized] target(s) in 0.05s
Running `target\release\mathru-rs.exe -l 10 -n 10`
Using f32 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.009277s(231.472Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.007753s(277.002Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.009030s(237.817Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.007585s(283.111Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.008559s(250.904Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.009235s(232.530Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.008425s(254.900Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.007451s(288.214Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.007609s(282.237Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.008545s(251.318Gflops)
Average Gflops: 258.950, Max Gflops: 288.214
Average Time: 0.008347s, Min Time: 0.007451s
PS D:\example\efficiency_v3\rust\mathru-rs> cargo run --release -- -l 10 -n 10 -d
Finished `release` profile [optimized] target(s) in 0.05s
Running `target\release\mathru-rs.exe -l 10 -n 10 -d`
Using f64 precision for matrix multiplication.
1 : 1024 x 1024 Matrix multiply wall time : 0.016261s(132.063Gflops)
2 : 1024 x 1024 Matrix multiply wall time : 0.016281s(131.904Gflops)
3 : 1024 x 1024 Matrix multiply wall time : 0.015308s(140.282Gflops)
4 : 1024 x 1024 Matrix multiply wall time : 0.016065s(133.672Gflops)
5 : 1024 x 1024 Matrix multiply wall time : 0.016702s(128.578Gflops)
6 : 1024 x 1024 Matrix multiply wall time : 0.014126s(152.019Gflops)
7 : 1024 x 1024 Matrix multiply wall time : 0.017731s(121.116Gflops)
8 : 1024 x 1024 Matrix multiply wall time : 0.020181s(106.409Gflops)
9 : 1024 x 1024 Matrix multiply wall time : 0.015631s(137.388Gflops)
10 : 1024 x 1024 Matrix multiply wall time : 0.015181s(141.459Gflops)
Average Gflops: 132.489, Max Gflops: 152.019
Average Time: 0.016347s, Min Time: 0.014126s
没有用到多线程,比ndarray快了不少,看来底层是进行了某些优化的。同样地,如果不考虑一维和二维数组之间的转换,实际计算性能应该会更高。
5. 总结
使用openmp、rayon等并行库加速的的C、fortran和rust矩阵乘法程序在使用相同算法的前提下,根据不同平台、编译器的实现,矩阵乘法的性能会有所些许区别,但总体上都在同一数量级。这种简单循环并行加速的计算方法适合矩阵规模较小的场合,随着矩阵规模的增加,整体计算性能愈发呈现下降的趋势。
即使采用分块矩阵+并行库的方法提高缓存命中率,性能提升依旧有限。而且矩阵分块大小与计算平台缓存大小有关,需要大量测试才能调出合适的分块参数。
使用fortran的matmul和rust的数学库实现的矩阵乘法功能,即使没有采用并行加速,其矩阵乘法性能依旧领先于简单循环并行加速的实现。这恰恰说明了底层算法优化的重要性。
在高性能计算领域除了openmp并行加速方法之外,还有blas、cuda、mpi等,将在以后的文章进一步演示。
